Hui-Shao's Blog

这几日，手上刚拿到了个 DIY 定制的 U盘，但由于自己的一些探索（作死）行为，U盘成功的寄了。

在抢救过程中，由于U盘采用的主控与颗粒的组合不太常见，在开卡时小坑无数，劳神费时，故有此篇记录。

最近在整理作业，发现这学期不知道自己怎么想的，竟然用中文序号来给文件命名，导致无法按文件名排序，属实是给自己挖坑了。

文件有好几十个，一个个去重命名费时费力，没办法，只能搓一个小小小程序辅助下了。

问题描述

AM（Amplitude Modulation），即幅度调制，常用于无线电载波传输讯息。

其基本原理是使用混频器，将低频的原始信号叠加到高频的载波信号上，使用低频信号对高频信号进行幅度调制，以传递信息。

考虑如下一个频率为 \(f_c\) ，幅度为 \(A\) 的正弦载波信号： \[ c\left( t \right) =A\cdot \cos \left( 2\pi f_ct \right) \] 另有一个调制波形（原始信号）： \[ m\left( t \right) =M\cdot \cos \left( 2\pi f_mt+\phi \right) \] 其中，$ f_m f_c $， \(M\) 是调制幅度，在确保 \(M<1\) 的前提下， \(1+m(t)\) 恒为正数，能够避免过调制现象产生。

前言

抖动如何产生？因为机械固有的物理特性，开关触点在瞬间接触的时候会有力学的回弹，使开关在“通”“断”之间反复横跳，造成 2-10 毫秒内信号不稳定。

在大部分情况下，这种信号抖动持续是没有影响的。但是当一个开关连接到一个足够“快”的电子设备上时，它可以检测到多次抖动并做出响应，那么就会引起问题。

在此，去除抖动的必要性就体现出来了。

最近在学数电，遇到了“竞争-冒险”现象。它在数字电路设计过程中常常会给输出带来意外的结果，成为数字电路设计中不得不考虑的一环。

故文章先从概念、分类说起，分析该现象产生的原因，提出判断是否存在“竞争-冒险”现象的方法，最后提供一些解决方案。

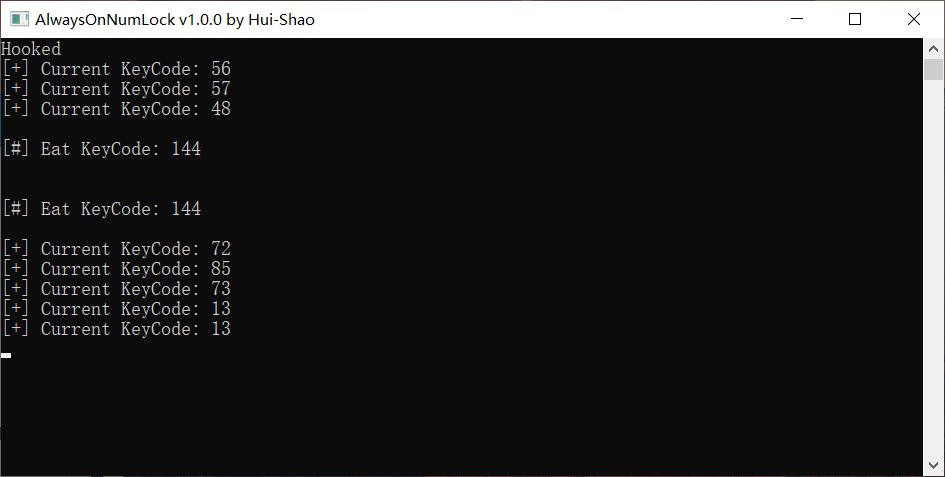
在使用键盘进行大量文字输入工作时，经常会不小心按到 NumLock 按键（尤其是在笔记本电脑上，Backspace 离它太近了），带来了不小的麻烦。

本次编写的小工具可以帮助你临时禁用 NumLock 按键。

问题引入

首先，我们考虑实变函数的情况，我们所要探究的是，下面的式子是否成立。 \[ \frac{d}{dy}\int_a^b{f\left( x,y \right) dx}=\int_a^b{\frac{\partial}{\partial y}f\left( x,y \right) dx} \tag{1} \label{1} \]

之后，我们再考虑复变函数的情况，探讨下面的式子是否成立。 \[ \frac{d}{dz}\oint_l{f\left( z \right) dz}=\oint_l{f'\left( z \right) dz} \tag{2} \label{2} \]

场效应管自身拥有众多优点，在常规电子电路以及集成电路上都有广泛的应用。

但由于其栅极的特点，以及高频次开关等工作要求，若是不加以保护，很容易损坏。

文章收集了一些常用的保护方式。

适当添加一点动效，能让博客显得没那么单调。

考虑到博客的背景图，在此引入一个下雪特效再合适不过了。

下面介绍一下使用 javascript 对这一效果的实现，以及添加特效到博客的过程。

安装依赖

1

pip install pillow

核心代码

新建一个 xxx.py 文件，写入：

1
2
3
4
5

from PIL import Image
import sys

with Image.open(sys.argv[1]) as im:
    im.save(input("目标文件名: "))